Fractal Geometry: Nature's Infinite Patterns
Fractal geometry is a branch of mathematics that explores the properties of fractals, which are complex geometric shapes that exhibit self-similarity at different scales.
published : 24 March 2024
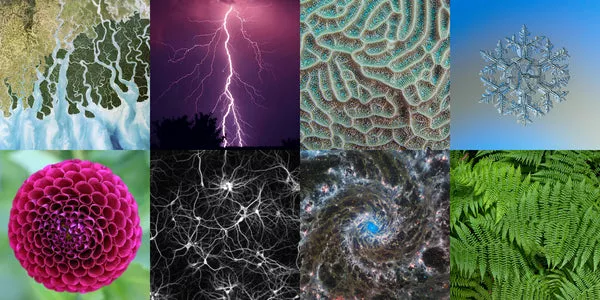
Fractal geometry is a branch of mathematics that explores the properties of fractals, which are complex geometric shapes that exhibit self-similarity at different scales. From the branching patterns of trees to the contours of coastlines, fractals are ubiquitous in nature and provide a fascinating glimpse into the infinite complexity of the natural world.
Basic Concepts
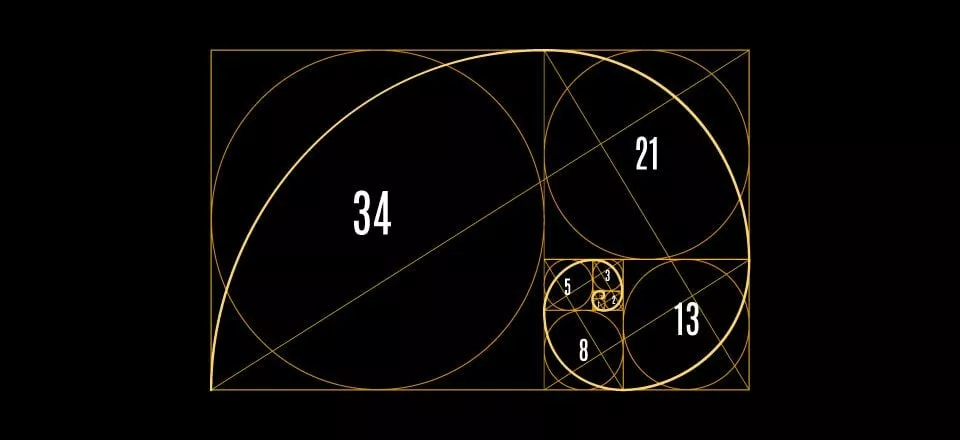
At the heart of fractal geometry are the concepts of self-similarity and iteration. A fractal is a geometric shape that appears similar at all levels of magnification, meaning that smaller parts of the fractal resemble the whole structure. This property of self-similarity allows fractals to exhibit intricate and detailed patterns at every scale.
Fractals are often generated through iterative processes, where a simple geometric shape is transformed repeatedly according to a set of rules. As the process is repeated, the fractal structure emerges, revealing complex patterns and structures that are characteristic of fractal geometry.
Applications
Fractal geometry has applications across diverse fields, including physics, biology, computer graphics, and finance. In physics, fractals are used to model and analyze complex systems such as turbulent fluid flows, chaotic dynamics, and fractal networks.
In biology, fractals are used to describe the branching patterns of trees, the structure of lungs and blood vessels, and the growth patterns of plants and animals. Fractal geometry provides insights into the underlying principles of biological form and function, from the microscopic to the macroscopic scale.
Computer Graphics
Fractal geometry has had a profound impact on computer graphics and digital art, inspiring new techniques for generating realistic and visually stunning images and animations. Fractal algorithms such as the Mandelbrot set and the Julia set have become iconic symbols of fractal geometry and have been used to create mesmerizing visualizations of complex mathematical structures.
Advancements in computational methods and computer technology have enabled artists and designers to explore the creative potential of fractal geometry, pushing the boundaries of digital art and animation. From generating intricate fractal landscapes to simulating natural phenomena such as clouds and terrain, fractal geometry continues to inspire new forms of artistic expression and digital media.
Modern Developments
In the modern era, fractal geometry continues to be a vibrant area of research with applications in various fields, including image processing, data analysis, and pattern recognition. Researchers are exploring new fractal algorithms and techniques for generating and analyzing complex patterns and structures.
Advancements in machine learning and artificial intelligence are enabling scientists and engineers to leverage fractal geometry for tasks such as image classification, object recognition, and data compression. Fractal-based algorithms are being used to extract meaningful patterns and features from large datasets and to enhance the performance of machine learning models.
Conclusion
Fractal geometry offers a mesmerizing journey into the infinite complexity of the natural world, revealing the intricate patterns and structures that abound in nature and mathematics. From its origins in the study of self-similarity and iteration to its modern applications in science, art, and technology, fractal geometry continues to captivate our imagination and inspire new discoveries and innovations.
As we marvel at the beauty and intricacy of fractal patterns in the world around us, let us appreciate the elegance and power of fractal geometry and the profound insights it provides into the underlying principles of nature, mathematics, and creativity.