Mathematical Logic: From Aristotle to Turing
Mathematical logic is a branch of mathematics that studies the principles of reasoning and the formal manipulation of symbols.
published : 20 March 2024
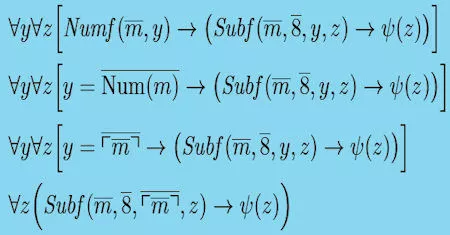
Mathematical logic is a branch of mathematics that studies the principles of reasoning and the formal manipulation of symbols. From its roots in ancient philosophy to its modern applications in computer science and artificial intelligence, mathematical logic has played a central role in shaping our understanding of logic and computation.
Historical Origins
The study of logic dates back to ancient times, with early philosophers such as Aristotle laying the groundwork for formal reasoning and deductive inference. Aristotle's syllogistic logic, which formalized the rules of deductive reasoning using categorical propositions and syllogisms, laid the foundation for later developments in mathematical logic.
In the 19th and early 20th centuries, mathematicians such as George Boole, Gottlob Frege, and Bertrand Russell made significant contributions to the development of modern mathematical logic. Boole's work on algebraic logic and Boolean algebra provided a formal framework for representing logical propositions and operations, while Frege's work on predicate logic introduced quantifiers and formalized the semantics of first-order logic.
Formal Systems
Mathematical logic is concerned with the study of formal systems, which are mathematical structures that capture the rules and principles of deductive reasoning. A formal system consists of a language, a set of axioms, and rules of inference.
The language of a formal system consists of symbols and formulas that represent logical propositions and statements. The axioms are self-evident truths or assumptions from which other statements can be derived, while the rules of inference specify how new statements can be derived from existing ones using logical reasoning.
Applications in Computer Science
In the 20th century, mathematical logic found applications in computer science and theoretical computer science, particularly in the development of algorithms, programming languages, and formal methods for reasoning about software and hardware systems.
One of the most influential developments in mathematical logic was the invention of the Turing machine by Alan Turing in the 1930s. The Turing machine laid the theoretical foundation for modern computing and formalized the concept of algorithmic computation, leading to the development of the theory of computability and complexity theory.
Modern Developments
In the modern era, mathematical logic continues to be a vibrant area of research with applications in various fields, including computer science, artificial intelligence, linguistics, and philosophy. Researchers are exploring new formal systems, logical calculi, and proof techniques to address emerging challenges in logic and computation.
Advancements in automated theorem proving, model checking, and formal verification are enabling engineers and scientists to verify the correctness of complex software and hardware systems and reason about their behavior with high confidence. Meanwhile, developments in artificial intelligence and machine learning are raising new questions about the nature of reasoning and intelligence, prompting researchers to revisit classical problems in logic and computation.
Conclusion
Mathematical logic is a rich and interdisciplinary field that spans ancient philosophy, modern mathematics, and contemporary computer science. From its origins in the logic of Aristotle to its modern applications in computer science and artificial intelligence, mathematical logic has provided a formal framework for reasoning about the principles of deduction, computation, and intelligence.
As we continue to explore the depths of mathematical logic and its applications, let us appreciate the enduring legacy of the great logicians and mathematicians who have shaped our understanding of logic and computation, from Aristotle to Turing and beyond.