Graph Theory: Exploring Connections

Graph theory is a branch of mathematics that studies the properties and relationships of graphs, which are mathematical structures.

published : 28 March 2024

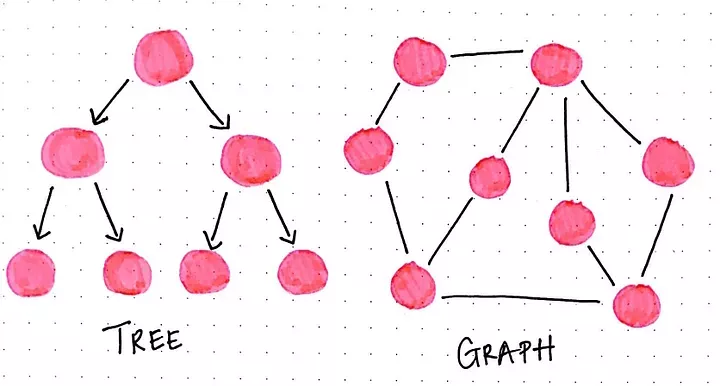
Graph theory is a branch of mathematics that studies the properties and relationships of graphs, which are mathematical structures that represent pairwise relationships between objects. From social networks and transportation systems to computer networks and biological networks, graphs provide a powerful framework for analyzing and understanding complex systems.

Basic Concepts

A graph consists of vertices (also known as nodes) and edges (also known as links or arcs) that connect pairs of vertices. Graphs can be directed or undirected, depending on whether the edges have a direction associated with them.

Graph theory encompasses various concepts and definitions, including paths, cycles, connectivity, and degrees of vertices. Paths are sequences of vertices connected by edges, while cycles are paths that form closed loops. Connectivity refers to the ability to reach any vertex from any other vertex via a path, while the degree of a vertex is the number of edges incident to it.

Applications

Graph theory has applications in diverse fields, including computer science, social sciences, biology, and operations research. In computer science, graphs are used to model and analyze data structures, algorithms, and networks.

In social sciences, graphs are used to model social networks, analyze interpersonal relationships, and study information diffusion and influence dynamics. In biology, graphs are used to model metabolic pathways, gene regulatory networks, and protein-protein interaction networks.

Graph Algorithms

Graph theory provides a rich set of algorithms for solving various problems on graphs, including shortest path algorithms, spanning tree algorithms, and graph traversal algorithms.

Shortest path algorithms, such as Dijkstra's algorithm and Bellman-Ford algorithm, find the shortest path between two vertices in a graph. Spanning tree algorithms, such as Prim's algorithm and Kruskal's algorithm, find a minimum spanning tree that connects all vertices in a graph with the minimum total edge weight.

Conclusion

Graph theory is a versatile and powerful tool for exploring connections and relationships in complex systems. By representing pairwise relationships between objects as graphs and applying graph algorithms and techniques, researchers gain insights into the structure, dynamics, and behavior of diverse systems.

As we continue to explore the depths of graph theory and its applications, let us remember the importance of connectivity and relationships in understanding the world around us and solving real-world problems.