Function Expression :
\[f(x)=x-\sqrt{x}.ln(x ) \]Domain
\[\left]0, \infty\right[ \]Limits
\[ \]Derivate
\[ \]Integral
\[F(x) = \frac{x^{2}}{2} - \begin{cases} - \frac{2 x^{\frac{3}{2}} \log{\left(\frac{1}{x} \right)}}{3} + \frac{2 x^{\frac{3}{2}} \log{\left(x \right)}}{3} - \frac{8 x^{\frac{3}{2}}}{9} & \text{for}\: \frac{1}{\left|{x}\right|} < 1 \wedge \left|{x}\right| < 1 \\\frac{2 x^{\frac{3}{2}} \log{\left(x \right)}}{3} - \frac{4 x^{\frac{3}{2}}}{9} & \text{for}\: \left|{x}\right| < 1 \\- \frac{2 x^{\frac{3}{2}} \log{\left(\frac{1}{x} \right)}}{3} - \frac{4 x^{\frac{3}{2}}}{9} & \text{for}\: \frac{1}{\left|{x}\right|} < 1 \\- {G_{3, 3}^{2, 1}\left(\begin{matrix} 1 & \frac{5}{2}, \frac{5}{2} \\\frac{3}{2}, \frac{3}{2} & 0 \end{matrix} \middle| {x} \right)} + {G_{3, 3}^{0, 3}\left(\begin{matrix} \frac{5}{2}, \frac{5}{2}, 1 & \\ & \frac{3}{2}, \frac{3}{2}, 0 \end{matrix} \middle| {x} \right)} & \text{otherwise} \end{cases} \]Sign Table

Variation Table

Plot
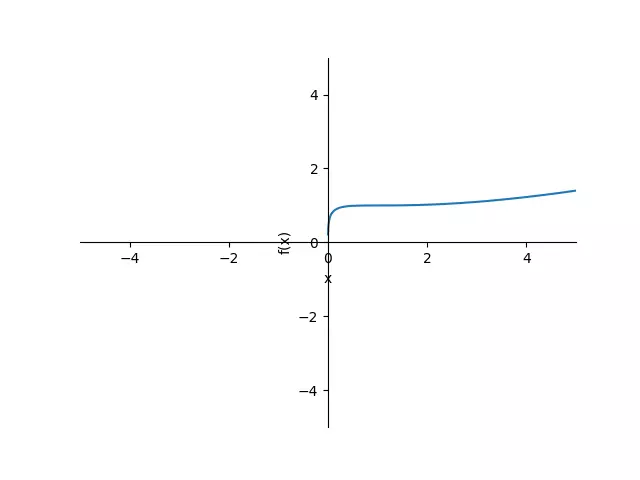
Elapsed Time: 0.0030 seconds